 Enfoques. Revista
de Investigación en Ciencias de la Administración http://doi.org/10.33996/revistaenfoques.v6i21.128 No. 21 | Volumen 6 | enero-marzo 2022
Enfoques. Revista
de Investigación en Ciencias de la Administración http://doi.org/10.33996/revistaenfoques.v6i21.128 No. 21 | Volumen 6 | enero-marzo 2022
http://revistaenfoques.org
ISSN: 2616 – 8219
ISSN-L: 2616 – 8219
pp. 106 – 116

Aplicación del Capital Asset Pricing Model para
conocer el Beta dentro del
mercado ecuatoriano
Application of the Capital
Asset Pricing Model
to know the Beta within
the Ecuadorian market Aplicação do Modelo de Precificação de Ativos de Capital para conhecer o Beta no mercado equatoriano
Fernando Neptalí
Terán Guerrero
Nery Elisabeth García Paredes
Viviana de Lourdes Vizcaino
Villavicencio
Mirian Noemi Carranza Guerrero
Artículo recibido el 1 de febrero
2022 | Aceptado el 3 de marzo 2022 | Publicado el 21 de enero 2022
Resumen
This
research develops the Capital Asset Pricing Model (CAPM), which is one of the most used and examined models in finance.
For the application of this model,
a sample of two shares considered in the ECUINDEX index within the Ecuadorian
stock market for the period 2016-2020 was obtained, to find the Beta for an
investor in Ecuador. In this model,
it is calculated taking into account variables such as the expected
profitability, risk of the actions, and that the portfolio finds the
appropriate Beta to make the investments, thus providing a useful tool when
investing in the Ecuadorian financial market. The investigation is of a correlational
type and a portfolio will be formed
that will be made up of the shares of Cervecería
Nacional, Corporación Favorita, which were able to obtain the information on the price of the
shares and achieving results where the Beta minimizes the risk in the best way. is the Favorite Corporation with a β = 1.9701, with a Ra =
4.92% and Cervecería Nacional with a β = 0.0517, with a Rb = 1.52% within the
Ecuadorian stock market. And the value of the portfolio was obtained at β = 1.0111,
with Rp = 3.22%, so we are balancing risk and return to make an investment in
these securities. The market risk premium is equal to 0.0177.
Palabras clave: Acciones; Beta; CAPM; inversión;
mercado
Abstract

Esta
pesquisa desenvolve o Modelo de Precificação de Ativos de Capital (CAPM), que é um dos modelos mais utilizados e examinados em finanças. Para a aplicação
deste modelo, foi obtida uma amostra de duas ações consideradas no índice
ECUINDEX dentro do mercado de ações equatoriano para o período 2016-2020, para
encontrar o Beta para um investidor no Equador.
Neste modelo, é calculado levando em consideração variáveis como a
rentabilidade esperada, risco das ações e que a carteira encontre o Beta
adequado para realizar os investimentos, fornecendo assim uma ferramenta útil
ao investir no mercado financeiro equatoriano. A investigação é de tipo
correlacional e será formada uma carteira que será composta pelas ações da
Cervecería Nacional, Corporación Favorita, que conseguiram obter a informação
sobre o preço das ações e obter resultados onde o Beta minimiza
o risco da melhor maneira.
é a Corporação Favorita
com β = 1,9701, com Ra = 4,92%
e Cervecería Nacional
com β = 0,0517, com Rb = 1,52% no mercado de ações equatoriano. E o valor da carteira
foi obtido em β = 1,0111, com Rp
= 3,22%, portanto
esta equilibrando risco
e retorno para fazer um investimento
nesses títulos. O prêmio de risco de mercado é igual a 0,0177.
Key words: Shares; Beta; CAPM; investment; market
RESUMO

Esta pesquisa desenvolve o Modelo de
Precificação de Ativos de Capital (CAPM), que é um dos modelos
mais utilizados e examinados
em finanças. Para a aplicação deste modelo, foi obtida uma amostra
de duas ações consideradas no índice ECUINDEX
dentro do mercado de ações equatoriano para o
período 2016-2020, para encontrar o Beta para um investidor no Equador. Neste modelo, é calculado levando
em consideração variáveis como a rentabilidade esperada, risco das ações e que
a carteira encontre o Beta adequado para realizar os investimentos, fornecendo
assim uma ferramenta útil ao investir no mercado financeiro equatoriano. A
investigação é de tipo correlacional e será formada uma carteira que será
composta pelas ações da Cervecería Nacional, Corporación Favorita, que
conseguiram obter a informação sobre o preço das ações e obter resultados onde
o Beta minimiza o risco da melhor maneira. é a Corporação Favorita com β =
1,9701, com Ra = 4,92% e Cervecería Nacional com β = 0,0517, com Rb = 1,52% no
mercado de ações equatoriano. E o valor da carteira foi obtido em β = 1,0111, com Rp
= 3,22%, portanto esta equilibrando risco
e retorno para fazer um investimento nesses títulos. O prêmio de risco de
mercado é igual a 0,0177.
Palavras-chave: ações; Beta; CAPM; investimento;
mercado
INTRODUCCIÓN
El presente
estudio tiene por objetivo analizar la aplicación del CAPM en el mercado
bursátil ecuatoriano, tomando como caso de estudio aplicación de dos
instrumentos financieros y el indicador de mercado. Desde un punto de vista
cronológico se debería iniciar citando “La Teoría
de Portafolio o Modelo de
Medias Varianzas” del investigador Markowitz (1952), que define en la teoría,
el hecho de que, el inversionista basa sus decisiones de acuerdo con la conformación óptima de su portafolio, es
decir, diversificando mediante el uso de indicadores como la media o rendimiento aritmético como medida de
rentabilidad y la varianza o desviación estándar como medidas de riesgos.
El modelo CAPM, es
sin duda, el que ha tenido mayor
aceptación hasta el día de hoy, debido
a que ofrece una predicción poderosa e intuitiva de cómo medir el riesgo y la
relación entre la tasa de retorno
esperada y el riesgo según mencionan (Fama y French, 2004). El investigador
Sharpe (1964), introduce para
este modelo un indicador de la volatilidad de un activo con
relación al mercado llamada “beta”, el
mismo que mide la sensibilidad de la rentabilidad del activo, frente a cambios
de rentabilidad suscitados en el mercado.
Este modelo
requiere de la existencia de un mercado de valores
desarrollado, ya que se sustenta en la teoría de los mercados
eficientes Mancera (2010), que indica que los precios de las acciones que
cotizan en las bolsas de valores reflejan toda la información pública relevante
de la empresa, de tal manera que, con solo saber la evolución de los precios de
las acciones de una compañía se puede inferir sobre su comportamiento pasado
y presente. La beta es un parámetro básico de medición del riesgo, dentro del
modelo CAPM de determinación de la rentabilidad mínima exigida por los
accionistas (Brealey, Allen y Myers, 2010).
Características de las acciones
Las acciones son
títulos de propiedad que emiten aquellas empresas constituidas en forma de
sociedad por acciones. Al vender las acciones, la empresa consigue incrementar
su capital, si se emite a la par (a su valor nominal), y también sus reservas,
si se emiten con prima (Pindado, 2012). Por tanto,
la emisión de las acciones incrementa los recursos propios de la
empresa; y estos recursos sirven como garantía para los acreedores, en caso de liquidación,
aunque también implican un aumento en el número de propietarios entre los que
hay que repartir los resultados que se obtengan.
Relación entre la rentabilidad de un
instrumento
financiero y el mercado
Un inversor que
acude a los mercados financieros con el objetivo de maximizar su rentabilidad y
minimizar el riesgo; sin embargo, este enfoque no permite estimar el
rendimiento que se debe esperar a la hora de invertir en un instrumento o
activo financiero ni, por tanto, determinar
el precio más adecuado para el activo. Si se enfoca
en los movimientos que experimentan los precios de diferentes
valores en un mercado, por ejemplo, empresas que cotizan en la Bolsa de Valores ecuatoriana, se puede observar que
tienden a moverse al alza o a la baja en conjunto y en el mismo sentido que en un índice del mercado como es el ECUINDEX.
El análisis de las
variaciones en el rendimiento de los instrumentos financieros y su relación con
el mercado que fue realizado por el investigador Sharpe (1964), en el conocido
como “modelo de mercado”. Según este modelo, el rendimiento de un instrumento financiero
se representa por la siguiente ecuación:
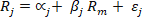
Donde, Rj es el rendimiento del título j, Rm es el rendimiento del mercado medida a través de un índice 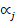 representa el instrumento
financiero cuando el rendimiento del índice de mercado es igual a cero,
representa el instrumento
financiero cuando el rendimiento del índice de mercado es igual a cero, 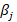 se
conoce como el coeficiente de volatilidad (pendiente de la recta) y
se
conoce como el coeficiente de volatilidad (pendiente de la recta) y 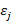 es el término aleatorio que
representa el error residual en la estimación del rendimiento.
es el término aleatorio que
representa el error residual en la estimación del rendimiento.
Se tiene la
posibilidad de realizar la inversión sin riesgo, al inversor le interesará
saber la rentabilidad que el título j le ofrece por encima del interés libre de
riesgo, o prima de riesgo. De este modo la ecuación siguiente se puede expresar como la relación entre la prima
de riesgo de un instrumento financiero y la prima de riesgo del mercado, y esta expresión
se la conoce como línea característica tiene la figura que se refiere a la línea característica (Fama y French, 2004).

Figura 1. Línea característica. Tomado de: Sharpe
(1964).
En la Figura 1
representa la rentabilidad que ofrece el activo por encima del interés libre de
riesgo en función del exceso de rentabilidad del mercado, la dispersión de los puntos expresa parte del rendimiento atribuible a las
características específicas del instrumento financiero o título valor.
El coeficiente β,
la pendiente de la línea característica se busca medir la sensibilidad del
rendimiento del título valor ante el rendimiento del mercado. Así que una
β > 1 se indica que el rendimiento del activo varía más que
proporcionalmente al rendimiento del mercado, se trata de activos “agresivos”. Mientras
que una β < 1 se denomina activos “defensivos”, su rendimiento se mueve en menor
proporción a la del mercado;
si los valores con β = 1 ofrecen una rentabilidad que varía en la misma
proporción que el del mercado. Por último, si algunos valores presentan una β
< 0 se trata de aquellos
instrumentos financieros cuyo rendimiento se mueve en dirección contraria al mercado,
se les denomina “super defensivos” (Ross, Westerfield y Jaffe, 2012)
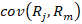 Como medida de variabilidad se tiene un método Bautista
(2013); Brealey et al. (2010),
para medir la beta de un título valor en función de la covarianza entre
el rendimiento del instrumento financiero y el rendimiento del
indicador del mercado, ,
y la varianza del rendimiento del mercado, según se menciona en la expresión siguiente:
Como medida de variabilidad se tiene un método Bautista
(2013); Brealey et al. (2010),
para medir la beta de un título valor en función de la covarianza entre
el rendimiento del instrumento financiero y el rendimiento del
indicador del mercado, ,
y la varianza del rendimiento del mercado, según se menciona en la expresión siguiente:
Cuando lo que se
desea, es estimar el rendimiento de un título valor para un periodo futuro se
tiene que considerar, que una variable
aleatoria cuyo valor esperado se
obtiene a partir de la siguiente expresión, dado que tanto αj como βj son constantes y E(εj) = 0, se tiene que:
Del mismo modo, a
partir de esta ecuación, se puede estimar el rendimiento esperado por encima
del interés libre de riesgo como:
La varianza de
dicha variable aleatoria será la siguiente:
Si se quiere
invertir en un portafolio diversificado de títulos, el modelo de mercado sirve
para estimar la respuesta de la rentabilidad y riesgo ante los movimientos del mercado. Para ello es
primordial se calcule
la beta de una cartera,
igual a la media ponderada de las betas de los títulos individuales que
la forman, con una ponderación igual a la proporción que representa cada título en la cartera Xj. Del mismo modo, la ordenada en el origen αj y la varianza del error aleatorio también se
calculan como la media ponderada (Sharpe, 1964).
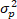 El rendimiento esperado E(Rp) y el riesgo de
una cartera formada por n títulos vendrá también determinado a partir de la línea característica de la
manera siguiente:
El rendimiento esperado E(Rp) y el riesgo de
una cartera formada por n títulos vendrá también determinado a partir de la línea característica de la
manera siguiente:
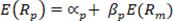
Al diversificar la
cartera se puede reducir e incluso eliminar, la variación del rendimiento que
se debe a las características específicas del valor, dejando solo las
variaciones que se deben a los movimientos del mercado en general, como se
puede ver en la Figura 2 (Sharpe, 1964).
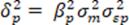
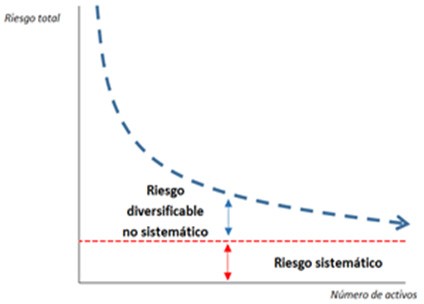
Figura
2. Riesgo de una cartera en función
del número de títulos.
Tomado
de: Sharpe (1964).
Estimación de la prima de riesgo del modelo
CAPM
A partir del
modelo de Markowitz y bajo el supuesto explícito de que los inversores se
comportan según sus prescripciones, tres autores Sharpe (1964), Linther (1965)
y Mossin (1966) desarrollaron un modelo conocido como CAPM (Capital Asset Pricing Model) que pretende
explicar cómo se forman los precios de los instrumentos financieros
cuando el mercado está en equilibrio. Estos
autores basan su modelo en una situación de equilibrio general de los
mercados de capitales que se asientan en un conjunto de hipótesis muy
restrictivas.
Existen dos métodos, la primera es SML versión covarianza, esta muestra la
relación de equilibrio entre la rentabilidad esperada y riesgo, medido a través
de la covarianza, para un título individual (Das, 2006). Esta relación se la
conoce como “Línea de Mercado
de Valores” o por las siglas SML
(Security Market Line). La ecuación expresada
es:
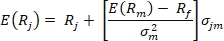
Otra forma
alternativa de expresar la covarianza de un valor es a través del coeficiente
de volatilidad β que mide el riesgo incremental que aporta una acción a una
cartera de valores diversificada. De este modo, es posible representar la línea de mercado de
valores como la relación entre E(RJ) y βj. La Figura 3 representa una versión de la SML como recta que pasa por dos puntos:
(1, E(Rm)) puesto
que la beta de la cartera de mercado
es
igual a 1; y el punto (0, Rj) la intersección vertical dado que la volatilidad del activo sin riesgo es igual
a 0 (Ross et al., 2012).
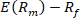 A la expresión se le
denomina “prima de riesgo del mercado” (ver Figura 3). Dado que E(Rm) y Rf no dependen del activo que se examina, el rendimiento esperado
de un título j en función de su coeficiente de
volatilidad βj aquellos
activos con betas más altas
ofrecerán rendimientos de
equilibrio mayores (Wong y Chirinos, 2016).
A la expresión se le
denomina “prima de riesgo del mercado” (ver Figura 3). Dado que E(Rm) y Rf no dependen del activo que se examina, el rendimiento esperado
de un título j en función de su coeficiente de
volatilidad βj aquellos
activos con betas más altas
ofrecerán rendimientos de
equilibrio mayores (Wong y Chirinos, 2016).

Figura
3. SML versión beta.
Tomado
de: Wong y Chirinos (2016)
MÉTODO
La presente
investigación fue de tipo cuantitativa, debido a que se aplicó una relación
numérica entre variables, y la probatoria de cálculos matemáticos. Para la respectiva aplicación del método de valoración de activos financieros, se realizó la extracción de datos de fuentes primarias, posteriormente se aplicó la
fórmula del CAPM con la finalidad de establecer los resultados.
La información
recopilada fue obtenida del sitio web de la Bolsa de Valores de Quito (BVQ), y los datos utilizados son de
frecuencia mensual y se refieren al período comprendido entre enero de 2015 y
diciembre de 2020 de las Compañías de
Corporación Favorita y Cervecería Nacional y el indicador del mercado bursátil
ECUINDEX (Bolsa de Valores de Quito, 2021).
El enfoque
de la investigación es correlacional, por la asociación de dos
variables que se encuentran vinculadas entre sí, en el cálculo de las
rentabilidades de los activos que se componen muestra que se utilizó los
precios de finales de cada mes de un total de acciones de empresas que han cotizado en bolsa
ecuatoriana en período considerado, y lo mismo se realiza con el indicador de ECUINDEX.
RESULTADOS
La Corporación
Favorita presenta un rendimiento promedio general mayor al mercado en conjunto,
en resumen, se presenta desde el periodo 2016-2020 (Figura 4).
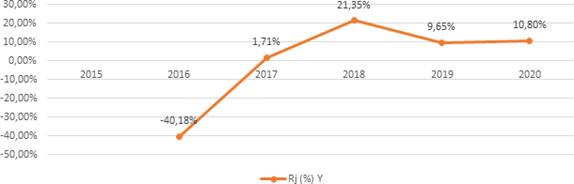
Figura
4. Rendimiento Corporación Favorita
2016 – 2020.
Tomado
de: Bolsa de Valores de Quito (2021).
La Cervecería Nacional presenta un rendimiento promedio general menor al del mercado en conjunto, en resumen,
presenta en la Figura 5 desde el periodo 2016-2020.
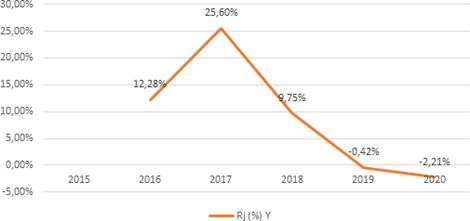
Figura
5. Rendimiento Cervecería Nacional
2016 – 2020.
Tomado
de: Bolsa de Valores de Quito (2021).
El
indicador ECUINDEX, con un promedio
en el rendimiento de Rm = 3,2014%,
se muestra en la Figura 6 desde el periodo 2016-2020.
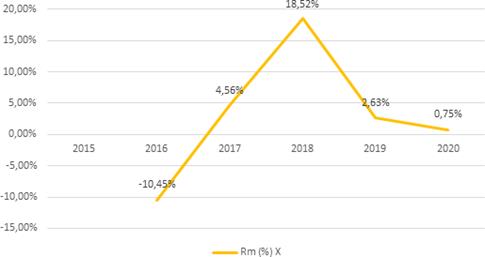
Figura 6. Rendimiento
ECUINDEX 2016 – 2020. Tomado de: Bolsa de Valores de Quito (2021).
Continuando con el
procedimiento a seguir para la aplicación del modelo CAPM para Ecuador
utilizado el caso de las Compañías de Corporación Favorita y Cervecería Nacional y el indicador del mercado
bursátil ECUINDEX y se procedió a obtener los datos
del precio de las acciones
dentro del mercado bursátil periodo 2016 -2220, luego se calculó todas las medidas de
variabilidad de cada compañía y se empezó con el supuesto que un inversionista
plantea diversificar su presupuesto al 50% entre los dos instrumentos
anteriormente mencionados. La Tabla 1
se presenta la siguiente información:
Tabla 1. Medidas
de variabilidad de Corporación Favorita en 2016-2020.
|
Año
|
Cotización
|
Rj (%) Y
|
Ecuindex
|
Rm (%) X
|
|
2015
|
3,10
|
|
1.199
|
|
|
2016
|
1,85
|
-40,18%
|
1.074
|
-10,45%
|
|
2017
|
1,89
|
1,71%
|
1.123
|
4,56%
|
|
2018
|
2,29
|
21,35%
|
1.331
|
18,52%
|
|
2019
|
2,51
|
9,65%
|
1.366
|
2,63%
|
|
2020
|
2,78
|
10,80%
|
1.376
|
0,75%
|
|
Rdto medio
|
|
0,0067
|
|
0,0320
|
|
Varianza ( )
|
|
0,0456
|
|
0,0086
|
|
Desv.Ti p (σ)
|
|
0,2136
|
|
0,0927
|
|
Covar (Rj,Rm)
|
|
0,0169
|
|
|
|
Beta
(β)
|
|
1,9704
|
|
|
En
la Tabla 1 la Corporación Favorita entre los años 2016
y 2020, muestra
un Ra= 0,67% y el Rm = 3,20%, una
σa =
21,36% y la σm = 9,27%, dando como
resultado un βa, m = 1,9794
que es mayor a 1 implica
que ante un aumento en el rendimiento del 1% del mercado, la acción mostrada un
rendimiento mayor, y por lo tanto si
su rendimiento es mayor, su riesgo
será menor.
Tabla 2. Medidas
de variabilidad de Cervecería Nacional en 2016-2020.
|
Año
|
Cotización
|
Rj (%) Y
|
Ecuindex
|
Rm (%) X
|
|
2015
|
58,69
|
|
1.199
|
|
|
2016
|
65,89
|
12,28%
|
1.074
|
-10,45%
|
|
2017
|
82,76
|
25,60%
|
1.123
|
4,56%
|
|
2018
|
90,83
|
9,75%
|
1.331
|
18,52%
|
|
2019
|
90,45
|
-0,42%
|
1.366
|
2,63%
|
|
2020
|
88,45
|
-2,21%
|
1.376
|
0,75%
|
|
Rdto medio
|
|
0,0900
|
|
0,0320
|
|
Varianza ( )
|
|
0,0100
|
|
0,0086
|
|
Desv.Ti p (σ)
|
|
0,1001
|
|
0,0927
|
|
Covar (Rj,Rm)
|
|
0,0004
|
|
|
|
Beta
(β)
|
|
0,0517
|
|
|
En la Tabla 2 la Cervecería Nacional entre los
años 2016 y 2020, muestra un Rb = 9% y el Rm = 3,20%, una σb = 10,01%
y la σm = 9,27%, dando como resultado un βb,m = 10,0517 que es
menor a 1 implica que el activo es
menos sensible que el índice y por tanto subirá y caerá menos que él.A partir
de esta información, el modelo de mercado permite calcular el riesgo
total, sistemático y específico para cada instrumento financiero, así como la cartera formada
por los dos títulos.
Tabla 3. Diversificación y riesgo total.
|
Títulos
|
Β
|
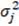
|
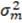
|
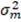
|
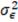
|
|
Corporación
Favorita
|
1,9704
|
0,0456
|
|
0,0333
|
0,0123
|
|
Cervecería Nacional
|
0,0517
|
0,0100
|
0,0086
|
0,00002
|
0,0100
|
|
Cartera
(50%)
|
1,0111
|
0,0144
|
|
0,0088
|
0,0056
|
La Tabla 3 se
muestra los riesgos para cada título y para la cartera formada por ambos.
Observa que la variabilidad del riesgo total se reduce cuando se combinan los
dos valores de Corporación Favorita y Cervecería Nacional, y en donde el riesgo
específico se reduce.
A partir
de la aplicación anterior se conoce que la beta de las acciones de
Corporación Favorita es de 1,9704,
la de Cervecería Nacional de 0,0517 y la de la Cartera con proporción de
inversión de un 50%, con lo que se da a conocer la rentabilidad a través del CAPM por un inversor
que desea invertir en estos instrumentos financieros, que servirá para que
pueda ser aplicado
por un inversor en otras
compañías del mercado bursátil
ecuatoriano, para continuar se requiere del interés libre de riesgo es del
1,43%, que es el rendimiento del Bono de Estados Unidos a 10 años como promedio
hasta el año 2020. La prima de riesgo del mercado será por
tanto igual a:
Y el cálculo el
CAPM para cada uno de los títulos y el portafolio, se obtiene las siguientes
rentabilidades esperadas que se sitúen sobre la recta SML representada en la
Figura 7.
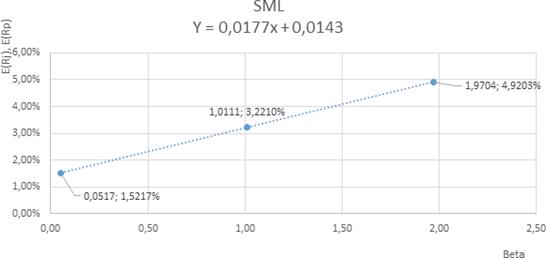
Figura 7. Aplicación del modelo CAPM a Corporación
Favorita, Cervecería Nacional y el portafolio.
CONCLUSIONES
Se definió que el
comportamiento de las empresas que cotizan en bolsa, se sugiere una correlación
observada entre los rendimientos de los instrumentos financieros se debe
en parte a su relación con una serie de factores comunes que pueden ser
representados a través del rendimiento del mercado.
La SML es una relación más importante del CAPM porque
define el riesgo de un título en términos de su contribución al riesgo del
portafolio de mercado.
Se enfocó que en
la investigación un valor de beta alto ofrece un rendimiento de equilibrio
mayor y un riesgo sistemático mayor por lo que los dos se mueven en conjunto,
la única forma de obtener rendimiento es a través del riesgo no diversificable, el cual depende
directamente de la beta del instrumento financiero. Los riesgos de cada tipo
de negocio no pueden ser los mismos, razón por
la cual, el modelo CAPM encuentra esta diferenciación de manera apropiada y
técnica a través del cálculo de la Beta.
No existe una verdad única o generalizada
sobre cual forma es mejor a la hora de obtener la beta de una empresa, hoy en
día incluso a la hora de valorar las empresas algunas
valoradores optan por tomar la
beta de una fuente secundaria con lo cual hacen caso omiso de los problemas que pueda tener esto.
REFERENCIAS
Bautista, R. (2013). Incertidumbre y
riesgos en decisiones de inversión. Bogotá: Ecoe Ediciones
Bolsa de Valores de Quito . (2021).
Portal de información. Obtenido de http://www. bolsadequito.com/index.php/mercados-
bursatiles/mercado-en-linea/rendimientos
Brealey, R., Allen, F.,
& Myers, S. (2010). Principios
Finanzas corporativas (9° ed). McGraw- Hill Education, México D.F
Das,
N. (2006). Los premios nobel de economia,
(4" ed). Bogotá: Piramide
Fama, E., y French, K. (2004). The Capital Asset Pricing Model: Theory and
Evidence. Journal of Economic Perspectives, 25-46
Linther, J. (1965). The Valuation
of Risk Assets and the Selection of Risky Investments in Stock Portfolios and
Capital Budgets. Review of Economics and Statistics, 47(1), 13-37
Mancera, A. (2010). Economía Internacional. Bogotá:
Patria
Markowitz, H. (1952). Portfolio
selection. The Journal of Finance, 77(1), 77-91
Mossin, J. (1966). Equilibrium in
Capital Asset Market. Econometrica, 768–783
Pindado, G. J. (2012). Finanzas Empresariales. Madrid: Paraninfo Editorial
Ross, S., Westerfield, R., y Jaffe,
J. (2012). Finanzas corporativas. (9° ed.). México
D.F.: McGraw-Hill Education
Sharpe, W. (1964). Capital Asset Prices: A Theory of Market Equilibrium
under conditions of risk. The
Journal of Finance, 19(3), 425-442
Wong, D., y Chirinos, M. (2016). ¿Los
modelos basados en el CAPM valoran adecuadamente los emprendimientos
familiares? Innnovar, 26(61), 65-82
 Enfoques. Revista
de Investigación en Ciencias de la Administración http://doi.org/10.33996/revistaenfoques.v6i21.128 No. 21 | Volumen 6 | enero-marzo 2022
Enfoques. Revista
de Investigación en Ciencias de la Administración http://doi.org/10.33996/revistaenfoques.v6i21.128 No. 21 | Volumen 6 | enero-marzo 2022![]()
![]()